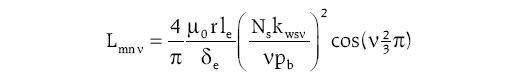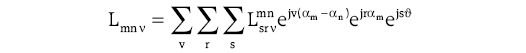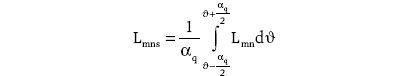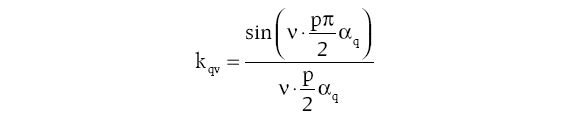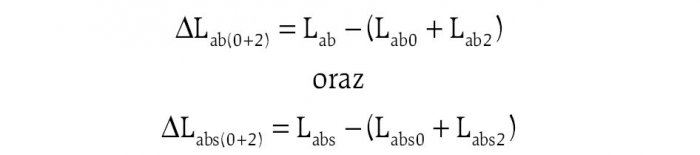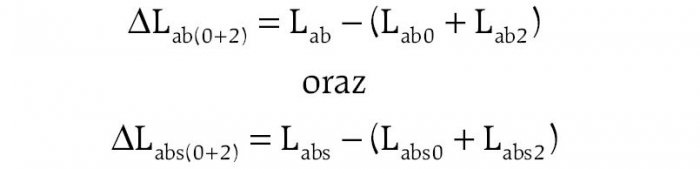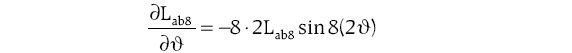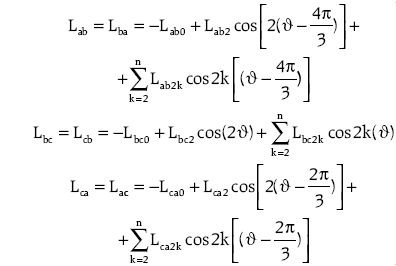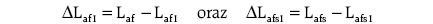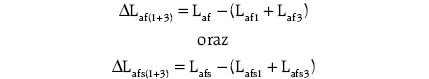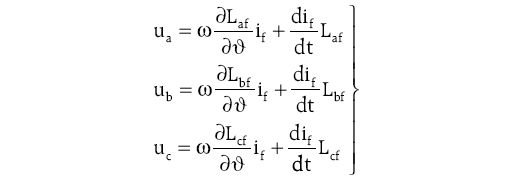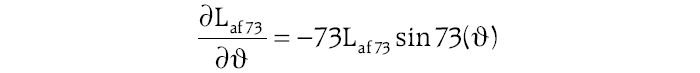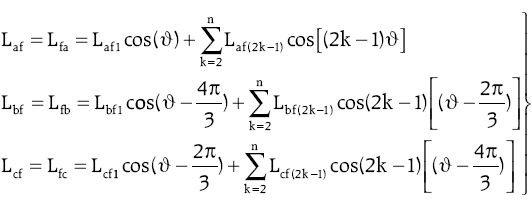Odwzorowanie indukcyjności wzajemnych w modelu obwodowym maszyny synchronicznej jawnobiegunowej
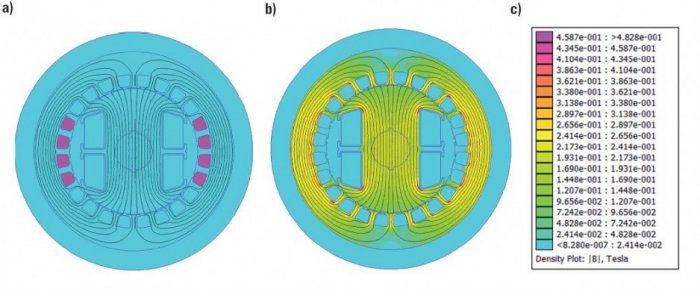
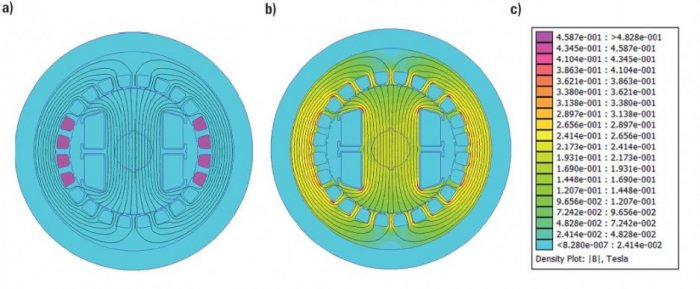
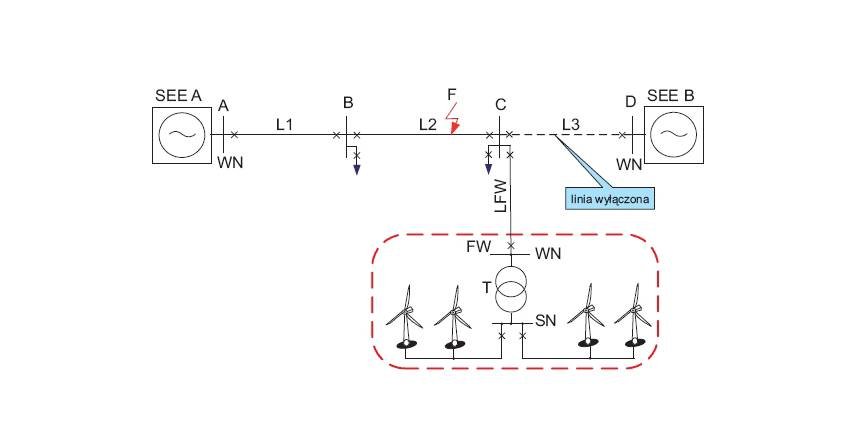
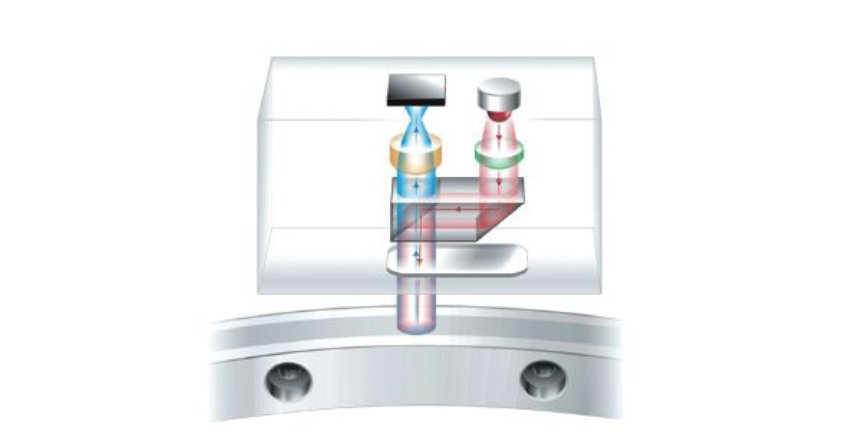
Rys. 1. Linie rozkładu a) pola magnetycznego generatora synchronicznego jawnobiegunowego od prądu 1 A płynącym w uzwojeniu pasmowym a stojana, b) rozkład gęstości pola magnetycznego B w poszczególnych częściach badanego generatora, c) wartości indukcji
K. Ludwinek
W równaniach strumieniowo-napięciowych opisujących model matematyczny maszyny synchronicznej jawnobiegunowej w układzie osi naturalnych związanych ze stojanem oraz z wirnikiem (bez obwodów tłumiących) z uwzględnieniem elektrycznego kąta położenia wirnika ϑ występują rozkłady:
indukcyjności własnych uzwojeń pasmowych stojana La, Lb, Lc oraz uzwojenia wzbudzenia Lf,
indukcyjności wzajemnych uzwojeń pasmowych stojana Lab, Lbc, Lca, Lba, Lcb, Lac.
indukcyjności wzajemnych uzwojeń pasmowych stojana i uzwojenia wzbudzenia Laf, Lbf, Lcf oraz Lbf, Lcf, Laf.
Zobacz także
AUTOMATION TECHNOLOGY Sp. z o.o. Automation Technology – nowy gracz na rynku

Automation Technology prężnie działa w obszarach energetyki, automatyki przemysłowej oraz robotyki.
Automation Technology prężnie działa w obszarach energetyki, automatyki przemysłowej oraz robotyki.
mgr inż. Dominik Trojnicz, dr hab. inż. Marcin Habrych, mgr inż. Justyna Herlender Wymagania stawiane automatyce zabezpieczeniowej i regulacyjnej inwerterów typu A
Obecny bardzo gwałtowny rozwój fotowoltaiki – nie tylko w Polsce, ale na całym terenie Unii Europejskiej (UE) – niesie za sobą dużo zalet, takich jak pozyskiwanie energii z praktycznie nieskończonej energii...
Obecny bardzo gwałtowny rozwój fotowoltaiki – nie tylko w Polsce, ale na całym terenie Unii Europejskiej (UE) – niesie za sobą dużo zalet, takich jak pozyskiwanie energii z praktycznie nieskończonej energii słonecznej oraz brak emisji szkodliwych gazów, co przyczynia się do redukcji emisji gazów cieplarnianych i zmniejszenia negatywnego wpływu na środowisko. Przyłączenie dużej liczby odnawialnych źródeł energii (OZE) nie pozostaje jednak bez wpływu na sieci elektroenergetyczne.
dr hab. inż. Marcin Habrych, mgr inż. Karol Świerczyński, dr inż. Bartosz Brusiłowicz Wymagania techniczne stawiane generacji rozproszonej w aspekcie elektroenergetycznej automatyki zabezpieczeniowej (część 2.)
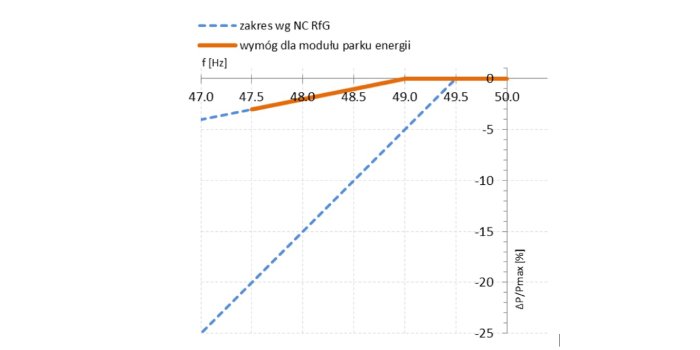
Odpowiedzią na wymagania stawiane przez Kodeks Sieciowy jest opracowanie przez Polskie Towarzystwo Przesyłu i Rozdziału Energii Elektrycznej (PTPiREE) na zlecenie Polskich Sieci Elektroenergetycznych (PSE)...
Odpowiedzią na wymagania stawiane przez Kodeks Sieciowy jest opracowanie przez Polskie Towarzystwo Przesyłu i Rozdziału Energii Elektrycznej (PTPiREE) na zlecenie Polskich Sieci Elektroenergetycznych (PSE) „Wymogów ogólnego stosowania wynikających z Rozporządzenia Komisji (UE) 2016/631 z dnia 14 kwietnia 2016 r., ustanawiającego Kodeks Sieci dotyczący wymogów w zakresie przyłączenia jednostek wytwórczych do sieci (NC RfG)” [4], opublikowanych w roku 2018.
StreszczenieW artykule przedstawiono sposób odwzorowania rozkładu indukcyjności wzajemnych uzwojeń pasmowych stojana i uzwojenia wzbudzenia w modelu obwodowym maszyny synchronicznej jawnobiegunowej bez skosu i ze skosem wirnika. Odwzorowanie rozkładu indukcyjności wzajemnych dokonano w funkcji kąta położenia wirnika na podstawie obliczonego rozkładu strumienia magnetycznego skojarzonego z dyskretnie rozłożonym uzwojeniem pasowym stojana oraz ze skupionym uzwojeniem wzbudzenia (przy uwzględnieniu rzeczywistej niesymetrii obwodu magnetycznego). Obliczenia rozkładu indukcyjności wzajemnych przeprowadzono za pomocą niekomercyjnego programu FEMM na podstawie danych konstrukcyjnych otrzymanych od producenta generatorów synchronicznych stosowanych w agregatach prądotwórczych.AbstractRepresentation of the mutual inductances in a circuital model of a salient-pole synchronous machineThe article concerns the representation of the mutual inductances of the stator and field windings in a circuital model of a salient-pole synchronous machine with and without a skew of the rotor. Representation of the self inductance are carried out as a function of the electrical rotor position angle on the basis of the calculated the magnetic flux distribution associated with discretely distributed stator windings and the concentrated field winding (with taking into account the real asymmetry of the magnetic circuit). Calculation of the mutual inductance distributions were carried out using noncommercial software FEMM on the basis of the real construction data received from a manufacturer of synchronous generators that are used in generator sets. |
Indukcyjności własne i wzajemne w modelu obwodowym w układzie współrzędnych naturalnych związanych ze stojanem i z wirnikiem można zapisać w postaci macierzowej Lsf jako [7]:
gdzie:
a, b i c – indeksy uzwojeń pasmowych stojana,
f – indeks uzwojenia wzbudzenia.
Jeśli szczelina powietrzna jest symetryczna, indukcyjności własne i wzajemne w macierzy (1) nie zależą od kąta położenia wirnika [8]. W przypadku niesymetrii występującej tylko po stronie stojana i równomiernej szczelinie po stronie wirnika dla v-tej harmonicznej przestrzennej uzwojenia pasmowego stojana, rozkład indukcyjności własnych opisano w pracach [8, 9]. W przypadku niesymetrii występującej po stronie stojana i wirnika rozkłady indukcyjności własnych uzwojeń pasmowych stojana La, Lb, Lc oraz dla uzwojenia wzbudzenia Lf, ich sposób odwzorowania dla v-tej harmonicznej przestrzennej dla modelu liniowego maszyny synchronicznej jawnobiegunowej został szczegółowo omówiony przez autora w artykule [6].
W wyrażeniu (1) indukcyjności własne są na tylko na przekątnej, pozostałe elementy macierzy stanowią indukcyjności wzajemne. W przypadku założenia równomiernej szczeliny powietrznej po stronie wirnika, indukcyjności wzajemne dla v-tej harmonicznej przyjmują stałe wartości i można przedstawić je według zależności [9]:
gdzie:
Ns – liczba zwojów uzwojenia pasmowego stojana,
kwsv – współczynnik uzwojenia,
pb – liczba par biegunów,
![]()
![]() – współczynniki amplitud składowej podstawowej oraz v-tej harmonicznej przestrzennej,
– współczynniki amplitud składowej podstawowej oraz v-tej harmonicznej przestrzennej,
m, n – indeksy pasma a, b, c, przy czym m≠n.
W przypadku nierównomiernej szczeliny powietrznej po stronie stojana i wirnika zmiana permeancji obwodu magnetycznego wirnika w osi podłużnej i poprzecznej względem uzwojeń pasmowych stojana powoduje, że indukcyjności wzajemne uzwojeń na stojanie (zależność (2)) będą zawierały dodatkowe składniki (oprócz składowej stałej) będące funkcją położenia wirnika ϑ względem osi uzwojeń stojana [8]. Indukcyjności wzajemne Lmnv będą zależeć od kąta położenia wirnika ϑ i dla v-tej harmonicznej przestrzennej w ogólnym przypadku można przedstawić je za pomocą potrójnego szeregu Fouriera [8]:
gdzie:
αm – jest połażeniem kątowym osi symetrii m-tego uzwojenia względem osi będącej odniesieniem na stojanie, np. osi uzwojenia pasma a,
αn – jest położeniem kątowym osi symetrii n-tego uzwojenia względem osi będącej odniesieniem na wirniku np. osi podłużnej,
r – indeks harmonicznej związanej z wirnikiem,
s – indeks harmonicznej związanej ze stojanem,
ϑ – oznacza elektryczne położenie kątowe osi odniesienia na wirniku względem osi odniesienia na stojanie, a zależność pomiędzy kątem elektrycznym J i kątem mechanicznym ϑm położenia wirnika wynosi ϑ=ϑmρb.
Dokładność obliczeń rozkładu indukcyjności wzajemnych wg (3) uzależniona jest od sposobu opisu funkcji uzwojeń i dla rzeczywistej maszyny synchronicznej jawnobiegunowej jest dość złożona. Dlatego często parametry elektromagnetyczne modeli matematycznych maszyn synchronicznych oblicza się za pomocą metod eksperymentalnych [5, 10] lub jeśli znane są wymiary geometryczne przy wykorzystaniu komercyjnych programów obliczających rozkład przestrzenny pola magnetycznego skojarzonego z danym uzwojeniem lub z uzwojeniami badanej maszyny elektrycznej. Najczęściej korzysta się z takich programów jak Flux, OPERA, Maxwell [1, 4, 11] itp., których zakup wiąże się z dużym wydatkiem finansowym. Rzadziej korzysta się z własnych programów [2, 3].
Dlatego w niniejszym artykule rozkłady indukcyjności wzajemnych uzwojeń pasmowych stojana Lab, Lbc, Lca, Lba, Lcb, Lac oraz indukcyjności wzajemne uzwojeń pasmowych stojana i uzwojenia wzbudzenia Laf, Lbf, Lcf oraz Lbf, Lcf, Laf dla modelu liniowego maszyny synchronicznej jawnobiegunowej wyznaczono za pomocą niekomercyjnego programu FEMM [1, 6, 12]. Wyznaczenie rozkładu indukcyjności wzajemnych dla modelu maszyny synchronicznej przeprowadzono dla generatora synchronicznego jawnobiegunowego (ze skosem i bez skosu wirnika) o danych znamionowych: SN=5,5 kVA, UN=400 V (Y), nN=3000 obr./min, IN=7.9 A, cosφN=0,8, liczba żłobków stojana Qs=24, ρb=1, kąt skosu wirnika αq =15°. Indukcyjności wzajemne zostały obliczone z uwzględnieniem rzeczywistych danych konstrukcyjnych (nierównomierna szczelina powietrzna na obwodzie stojana i wirnika), jakie autor otrzymał od producenta generatorów synchronicznych jawnobiegunowych stosowanych w agregatach prądotwórczych. W obliczeniach uwzględniono jednowarstwowe uzwojenie, jakie fabrycznie zostało ułożone w żłobkach stojana badanej maszyny synchronicznej jawnobiegunowej. Efekt skosu w programie FEMM uzyskano poprzez podział długości wirnika na 15 elementów (tzw. „plastrów”). Każdy z tych elementów względem poprzedniego wzdłuż długości wirnika przesunięto o kąt 1° i dla każdego „plastra”, czyli nowego ustawienia wirnika, należy powtórzyć obliczenia. Indukcyjność ze skosem oblicza się wykonując całkowanie według zależności:
gdzie:
m, n – indeksy pasma a, b, c stojana oraz wirnika,
ϑ – kąt elektryczny wzdłuż obwodu magnetycznego,
αq – kąt skosu,
Lmns – rozkład indukcyjności ze skosem,
Lmn – rozkład indukcyjności bez skosu.
Z uwagi na przyjętą symetrię rozłożenia uzwojeń pasmowych stojana oraz liniowość obwodu magnetycznego, rozkłady indukcyjności wzajemnych uzwojeń stojana Lab, Lbc, Lca – ze skosem wirnika są takie same jak odpowiadające im indukcyjności wzajemne Lba, Lcb, Lac. Podobnie rozkłady indukcyjności wzajemnych ze skosem wirnika Labs, Lbcs, Lcas są takie same jak odpowiadające im indukcyjności wzajemne Lbas, Lcbs, Lacs.
Założenie symetrii uzwojeń pasmowych stojana i liniowości obwodu magnetycznego badanego generatora synchronicznego powoduje, że rozkłady indukcyjności wzajemnych uzwojenia wzbudzenia i uzwojeń pasmowych stojana są takie same zarówno dla przypadku wytworzenia pola magnetycznego od strony uzwojenia wzbudzenia, jak i od strony uzwojenia stojana. Oznacza to, że w macierzy (1) rozkłady indukcyjności Laf, Lbf, Lcf (bez skosu wirnika) mogą być zastąpione rozkładem indukcyjności Lfa, Lfb, Lfc i vice versa. Podobnie Lafs, Lbfs, Lcfs (ze skosem wirnika) są takie same jak Lfas, Lfbs, Lfcs.
Na rysunku 1. przedstawiono linie rozkładu pola magnetycznego od prądu 1 A płynącego w uzwojeniu pasmowym a stojana (4 górne żłobki i 4 dolne żłobki) wraz z widokiem gęstości indukcji B. Na rysunku 1. widoczne jest początkowe położenie wirnika ϑ0=0.
Indukcyjności wzajemne uzwojeń pasmowych stojana
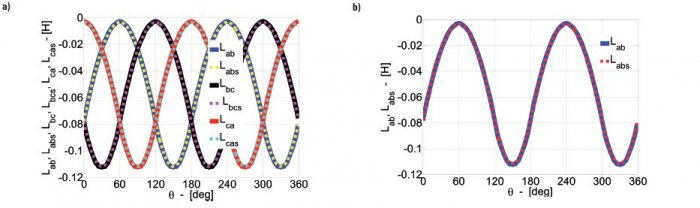
Na rysunku 2. przedstawiono rozkład indukcyjności wzajemnych uzwojeń pasmowych stojana Lab (Lba), Lbc (Lcb), Lca (Lac) z wirnikiem bez skosu oraz Labs (Lbas), Lbcs (Lcbs), Lcas (Lacs) ze skosem wirnika w funkcji zmian elektrycznego kąta położenia wirnika ϑ.
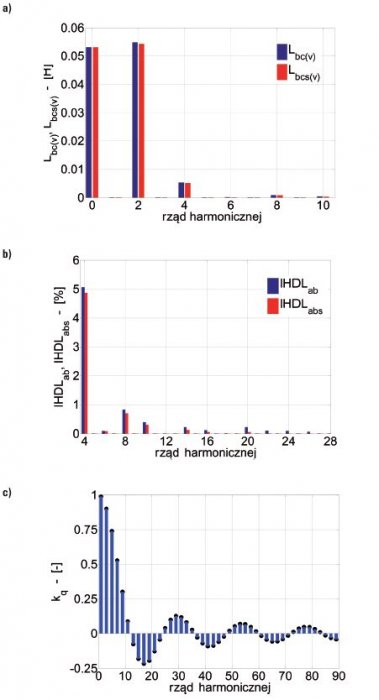
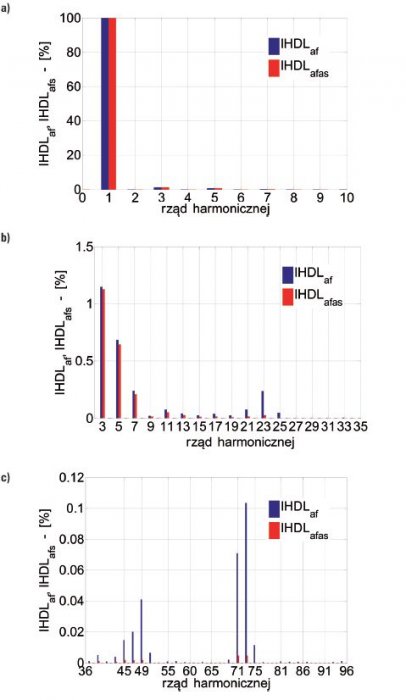
Przedstawione na rysunku 2. rozkłady indukcyjności wzajemnych uzwojeń pasmowych stojana oprócz składowej stałej są również odkształcone niesymetrią magnetyczną obwodu wirnika. Podczas jednego obrotu wirnika o kąt elektryczny 360° dwukrotna zmiana przewodności magnetycznej (w osi podłużnej i poprzecznej wirnika – rys. 1.), jaka pojawia się w osi każdego uzwojenia pasmowego stojana, powoduje powstanie widocznego (na rys. 2.) większego udziału amplitudy 2. harmonicznej niż składowej stałej wynikającej z zależności (2). Rozkłady indukcyjności wzajemnej Lab (bez skosu wirnika) oraz Labs (ze skosem wirnika) poddano analizie Fouriera. Na rysunku 3. przedstawiono zawartości amplitud wyższych harmonicznych dla rozkładów indukcyjności wzajemnej Lab oraz Labs oraz tłumiące działanie skosu wirnika (dla αq=15°) na v-tą harmoniczną przestrzenną.
Z porównania zawartości wyższych harmonicznych amplitud rozkładów indukcyjności wzajemnej uzwojeń pasmowych stojana (rys. 3.) wynika, że zarówno dla generatora synchronicznego ze skosem wirnika, jak i bez skosu w rozkładach dominuje składowa stała oraz wyższe harmoniczne parzyste, w tym najbardziej znacząca 2. harmoniczna z udziałem 105% (względem składowej stałej). Ponadto występują 4. harmoniczna z udziałem 9,5% oraz 8. harmoniczna z udziałem 1,6%. Pozostałe wyższe harmoniczne nie przekraczają 0,4%. Z przedstawionego na rysunku 3. spektrum amplitud rozkładów indukcyjności wzajemnych uzwojeń pasmowych stojana wynika tłumiące działanie skosu wirnika, które określa współczynnik skosu wirnika kq względem żłobków stojana (rys. 3c). Dla v-tej harmonicznej przestrzennej współczynnik skosu wirnika opisany jest wyrażeniem [6, 9]:
gdzie:
αq – kąt skosu wirnika liczony wzdłuż jego długości. Współczynnik ten przyjmuje wartości zero dla argumentu ![]() , gdzie k jest liczbą całkowitą. Skos wirnika o kąt elektryczny αq=15° (jak to ma miejsce dla 24 żłobków stojana badanego generatora) spowoduje, że zerowaniu ulegają przestrzenne harmoniczne rzędu 12. i jej wielokrotności tj. 24., 36., 48. ... (rys. 3c). Z uwagi na niewielki udział wyższych harmonicznych (w dodatku tylko niższego rzędu) w rozkładzie indukcyjności wzajemnych uzwojeń pasmowych stojana (rys. 3.) działanie tłumiące skosu wirnika jest bardzo słabo widoczne.
, gdzie k jest liczbą całkowitą. Skos wirnika o kąt elektryczny αq=15° (jak to ma miejsce dla 24 żłobków stojana badanego generatora) spowoduje, że zerowaniu ulegają przestrzenne harmoniczne rzędu 12. i jej wielokrotności tj. 24., 36., 48. ... (rys. 3c). Z uwagi na niewielki udział wyższych harmonicznych (w dodatku tylko niższego rzędu) w rozkładzie indukcyjności wzajemnych uzwojeń pasmowych stojana (rys. 3.) działanie tłumiące skosu wirnika jest bardzo słabo widoczne.
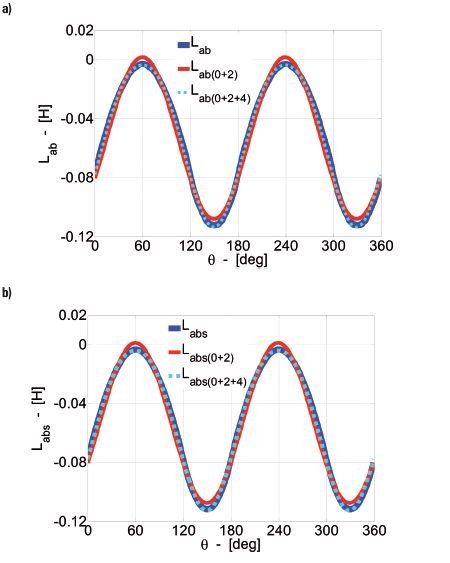
Często w obliczeniach numerycznych rozkłady indukcyjności wzajemnych Lab, Lbc, Lca (lub Lba, Lcb, Lac) – ze skosem wirnika oraz Labs, Lbcs, Lcas (Lbas, Lcbs, Lacs) – bez skosu odwzorowuje się za pomocą składowej stałej i 2. harmonicznej. Odwzorowanie indukcyjności własnych Lab i Labs sumą składowej stałej i 2. harmoniczną (Lab0 +Lab2 oraz Labs0 +Labs2) oraz sumą Lab0 + Lab2 + Lab4 i Labs0 + Labs2 + Labs4, tzn. z uwzględnieniem również 4. harmonicznej przedstawia rysunek 4.
Przy odwzorowaniu indukcyjności wzajemnych zdecydowano się wyznaczyć tylko ich różnice bezwzględne, gdyż próba obliczenia błędu względnego δLab wprowadza nieokreśloność wyrażenia na błąd względny. Nieokreśloność ta wynika z przemiennego charakteru rozkładu indukcyjności wzajemnej Lab oraz Labs, a więc i występowaniu wartości zero w mianowniku.
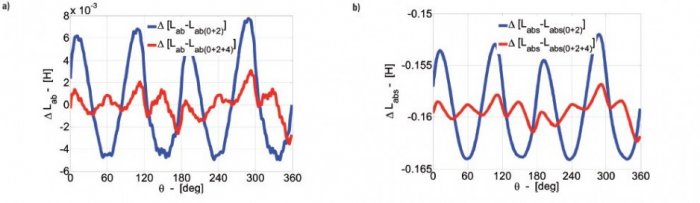
Na rysunku 5. przedstawiono rozkład różnic występujących przy odwzorowaniu indukcyjności wzajemnej uzwojeń pasmowych stojana ΔLab dla wirnika bez skosu oraz ΔLabs ze skosem:
§ ΔLab (0+2) oraz ΔLabs (0+2) – rozkłady będące różnicą indukcyjności wzajemnej uzwojenia pasmowego stojana oraz sumy jej składowej stałej i 2. harmonicznej:
- ΔLab (0+2+4) oraz ΔLabs (0+2+4) – rozkłady będące różnicą indukcyjności wzajemnej uzwojenia pasmowego stojana oraz sumy jej składowej stałej, 2. i 4. harmonicznej:
Zarówno dla wirnika ze skosem, jak i bez skosu maksymalne różnice odwzorowania rozkładu indukcyjności wzajemnych uzwojeń pasmowych stojana wynoszą:
- w przypadku sumy Lab0 i Lab2 różnica nie przekracza 8 mH (16% względem składowej stałej Lab0),
- w przypadku sumy Lab0, Lab2 i Lab4 różnica nie przekracza 2 mH (4% względem składowej stałej Lab0).
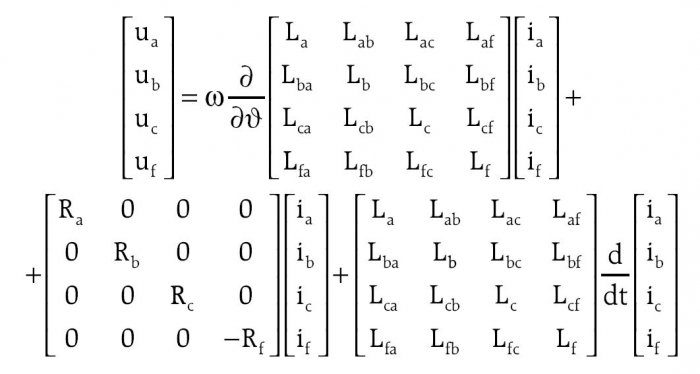
Pomimo dobrego odwzorowania indukcyjności wzajemnych uzwojeń pasmowych stojana (rys. 4. i 5.) sumą składowej stałej i 2. harmonicznej oraz sumą składowej stałej, 2. i 4. harmonicznej (uwzględnienie szerszego spektrum wyższych harmonicznych przestrzennych w rozkładach indukcyjności wzajemnych uzwojeń pasmowych stojana jest ważne, gdyż w modelu obwodowym generatora synchronicznego określonym zależnością [7]:
wymagane jest również obliczanie pochodnych z rozkładów indukcyjności określonych macierzą (1), gdzie:
a, b i c – indeksy uzwojeń pasmowych stojana,
f – indeks uzwojenia wzbudzenia,
Ra, Rb, Rc – rezystancje uzwojeń pasmowych stojana,
Rf – rezystancja uzwojenia wzbudzenia,
isf=[ia, ib, ic, if]T – macierz prądów pasmowych stojana i uzwojenia wzbudzenia,
usf=[ua, ub, uc, uf]T – macierz napięć fazowych uzwojeń pasmowych stojana oraz napięcia uzwojenia wzbudzenia,
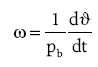
 – elektryczna prędkość kątowa,
– elektryczna prędkość kątowa,
pb – liczba par biegunów.
Z przedstawionego spektrum harmonicznych (rys. 3.) widać, że dla maszyny synchronicznej jawnobiegunowej bez skosu wirnika przykładowo udział 8. harmonicznej wynosi 0,9% (względem składowej stałej) i jest wprawdzie niewielki, ale w przypadku obliczania pochodnej w zależności (7) jej wartość zostanie wzmocniona poprzez wartość wynikającą z rzędu pochodnej, np. dla pasma a i b pochodna 8. harmonicznej wyniesie:
osiągając w składniku pierwszym zależności (7) znacznie większe wartości niż dla 8. harmonicznej indukcyjności wzajemnej uzwojeń stojana w składniku 3 zależności (7). Ponadto, z zależności (7) wynika, że pochodne indukcyjności są wzmacniane wartością elektrycznej prędkości kątowej w, która dla częstotliwości 50 Hz wynosi 100p. Pochodne indukcyjności wzajemnych Lab, Lbc, Lca (lub Lba, Lcb, Lac) będą miały wpływ na przebieg napięć fazowych w stanie obciążenia generatora synchronicznego.
Na podstawie rysunków 2–4 można utworzyć zależności opisujące przestrzenny rozkład indukcyjności własnych uzwojeń pasmowych stojana generatora synchronicznego jawnobiegunowego ze skosem i bez skosu wirnika w funkcji kąta położenia wirnika ϑ[7].
Indukcyjności wzajemne uzwojeń pasmowych stojana i wzbudzenia
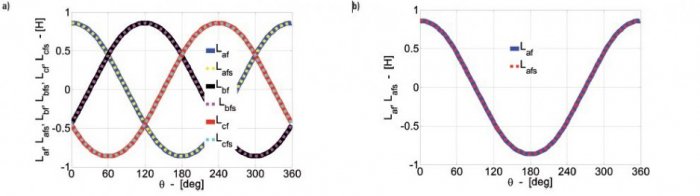
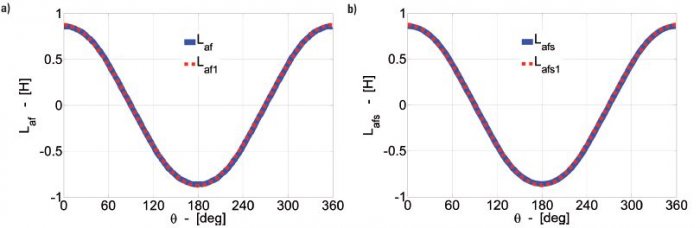
Na rysunku 6. przedstawiono rozkłady indukcyjności wzajemnych Laf,Lbf, Lcf (lub Lafs,Lbfs, Lcfs), które obrazują zmiany wartości indukcyjności wzajemnych występujące pomiędzy uzwojeniami pasmowymi stojana i skupionym uzwojeniem wzbudzenia oraz pomiędzy skupionym uzwojeniem wzbudzenia i uzwojeniami pasmowymi stojana. W rozkładach tych uwzględniono niesymetrię magnetyczną wirnika (w osi podłużnej i poprzecznej) oraz nierównomierności szczeliny powietrznej stojana i wirnika.
Przedstawione rozkłady (rys. 6.) są prawie sinusoidalne, tzn. o niewielkiej zawartości wyższych harmonicznych. Rozkład indukcyjności wzajemnych Lbf (oraz Lfb) jest przesunięty w o 120° elektrycznych względem rozkładów indukcyjności wzajemnej Laf (oraz Lfa), natomiast indukcyjność Lcf (oraz Lfc) jest przesunięta o 240° elektrycznych względem Laf. Rozkłady indukcyjności wzajemnych Laf i Lafs (rys. 6.) poddano analizie Fouriera. Na rysunku 7. przedstawiono zawartość wyższych harmonicznych amplitud rozkładów indukcyjności wzajemnej Laf (bez skosu wirnika) i Lafs (ze skosem wirnika). Procentowy udział liczono względem składowych podstawowych Laf1 i Lafs1.
Z porównania zawartości wyższych harmonicznych amplitud indukcyjności wzajemnej uzwojeń pasmowych stojana i uzwojenia wzbudzenia (rys. 7.) wynika, że w rozkładach dominuje składowa podstawowa indukcyjności wzajemnych oraz o bardzo niewielkim udziale wyższe harmoniczne nieparzyste. Przykładowo najbardziej znacząca 3. harmoniczna Laf3 (Lafs3) ma udział 1,2%, a 5. harmoniczna ma udział 0,65%. Pozostałe wyższe harmoniczne nie przekraczają 0,25%. Z przedstawionego rozkładu zawartości wyższych harmonicznych (rys. 7.) wynika, że najprostsze odwzorowanie rozkładu indukcyjności wzajemnych uzwojeń pasmowych stojana i wzbudzenia Lab (bez skosu) oraz Labs (ze skosem) można dokonać za pomocą składowej podstawowej Laf1 (Lafs1), co przedstawia rysunek 8.
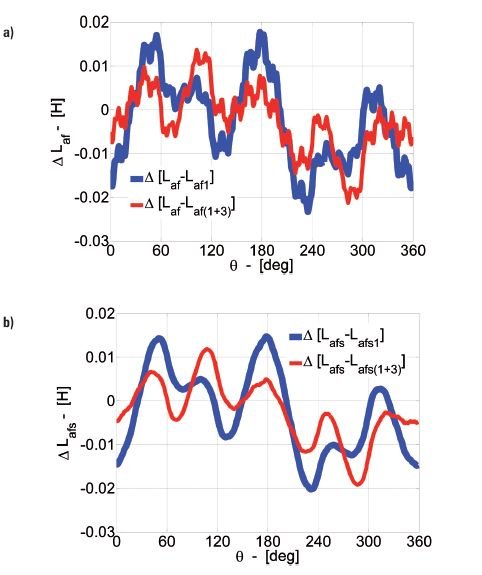
Na rysunku 9. przedstawiono rozkłady różnic występujących przy odwzorowaniu indukcyjności wzajemnej uzwojeń pasmowych stojana i wzbudzenia ΔLaf dla wirnika bez skosu oraz ΔLafs ze skosem:
- DLaf1 oraz DLabs1 – rozkłady będące różnicą indukcyjności wzajemnej uzwojenia pasmowego stojana i wzbudzenia oraz jej składowej podstawowej Laf1:
- DLaf (1+3) oraz DLafs (1+3) – rozkłady będące różnicą indukcyjności wzajemnej uzwojenia pasmowego stojana i wzbudzenia oraz sumy jej składowej podstawowej i trzeciej harmonicznej Laf3:
Porównując z rysunku 7. rozkłady widać, że maksymalne różnice odwzorowania indukcyjności wzajemnych uzwojenia pasmowego stojana ΔLaf dla generatora z wirnikiem bez skosu oraz ΔLafs ze skosem wirnika:
§ za pomocą tylko składowej podstawowej nie przekraczają 17 mH, tj. 2% względem składowej podstawowej Laf1 (dla ΔLaf) oraz nie przekraczają 15 mH, tj. 1,7% względem składowej podstawowej Lafs1 (dla ΔLafs),
§ przy uwzględnieniu sumy składowej podstawowej i trzeciej harmonicznej nie przekraczają 14 mH, tj. 1,6% względem składowej podstawowej Laf1 (dla ΔLaf) oraz nie przekraczają 12 mH, tj. 1,4% względem składowej podstawowej Lafs1 (dla ΔLafs).
Uwzględnienie szerszego spektrum wyższych harmonicznych w rozkładach indukcyjności wzajemnej uzwojeń pasmowych stojana i uzwojenia wzbudzenia niż tylko najbliższych harmonicznych leżących w pobliżu składowej podstawowej szczególniwe dla maszyn synchronicznych bez skosu wirnika Laf (ϑ) jest ważniejsze niż opisane wcześniej obliczanie pochodnych w rozkładach indukcyjności wzajemnej uzwojeń pasmowych stojana. Na podstawie przyjętych zawartości wyższych harmonicznych w rozkładach indukcyjności Laf (ϑ) (rys. 7.) liczone są ich pochodne, których udział w indukowanych napięciach w uzwojeniach pasmowych stojana, np. w stanie biegu jałowego jest największy. Wartości indukowanych napięć fazowych w stanie biegu jałowego dla modelu obwodowego maszyny synchronicznej jawnobiegunowej na podstawie zależności (7) można zapisać jako:
Z przedstawionego na rysunku 7. spektrum harmonicznych rozkładu indukcyjności wzajemnych widać, że dla maszyny synchronicznej jawnobiegunowej bez skosu wirnika, przykładowo udział 73. harmonicznej wynosi 0,1% (względem składowej podstawowej) i jest wprawdzie niewielki, ale w przypadku obliczania pochodnej występującej w wyrażeniu (7) i (11) jej wartość zostanie wzmocniona 73 razy (poprzez wartość wynikającą z rzędu pochodnej, np. dla uzwojenia stojana pasma a i uzwojenia wzbudzenia pochodna wynosi:
Jak widać, jej udział wzrośnie do 7,3% (amplitudy składowych podstawowych rozkładu indukcyjności uzwojeń pasmowych stojana i uzwojenia wzbudzenia i ich pochodnych są takie same). Z zależności (11) wynika, że w przebiegach czasowych indukowanych napięć fazowych w uzwojeniach stojana w stanie biegu jałowego najbardziej widoczny będzie wpływ pochodnych indukcyjności wzajemnych uzwojeń pasmowych stojan i wzbudzenia.
Na podstawie przedstawionych rozkładów indukcyjności wzajemnych uzwojeń pasmowych stojana i uzwojenia wzbudzenia ze skosem i bez skosu wirnika (rys. 6.) oraz ich widma amplitudowego można utworzyć następujące zależności w funkcji kąta położenia wirnika J:
Podsumowanie
W artykule przedstawiono udział zawartości wyższych harmonicznych w opisie rozkładów indukcyjności wzajemnych dyskretnie rozłożonych uzwojeń pasmowych stojana i skupionego uzwojenia wzbudzenia dla liniowego modelu maszyny synchronicznej jawnobiegunowej ze skosem i bez skosu wirnika. Indukcyjności wzajemne wyznaczono za pomocą niekomercyjnego programu FEMM w funkcji elektrycznego kąta położenia wirnika na podstawie obliczonego rozkładu strumienia magnetycznego skojarzonego z uzwojeniami pasowymi stojana oraz z uzwojeniami stojana i wzbudzenia dla rzeczywistych danych konstrukcyjnych generatora synchronicznego jawnobiegunowego o mocy 5,5 kVA.
Jak przedstawiono w artykule, program FEMM 2D umożliwia również wyznaczenie rozkładu indukcyjności wzajemnych z uwzględnieniem skosu wirnika. Do tego celu wykorzystano własny program napisany w języku skryptowym LUA, który umożliwia automatyczną zmianę położenia wirnika o zadany kąt i kilkukrotne powtórzenie obliczeń z jednoczesnym zapisem wyników. Ostatnie obliczenie przeprowadza się dla końcowego kąta skosu wirnika aq. W przypadku zastosowania programów 2D (np. FEMM lub Flux 2D itp.) obliczone indukcyjności wzajemne należy powiększyć o indukcyjności połączeń czołowych uzwojeń.
Przedstawione w niniejszym artykule rozkłady indukcyjności wzajemnych oraz ich zawartości wyższych harmonicznych pozwalają w prosty sposób uwzględniać harmoniczne o największym udziale i sformułować opisy matematyczne indukcyjności wzajemnych, a szczególnie ich pochodnych, występujące w modelach obwodowych generatorów synchronicznych jawnobiegunowych.
Z przedstawionych rozważań dotyczących sposobu odwzorowania zawartości wyższych harmonicznych wynika, ze wprowadzenie skosu eliminuje w rozkładzie indukcyjności wzajemnych szczególnie harmoniczne wyższych rzędów. W przypadku modeli matematycznych generatorów synchronicznych bez skosu wirnika o udziale danej harmonicznej np. w indukowanych napięciach pasmowych w mniejszym stopniu decydować będzie amplituda v-tej harmonicznej rozkładu indukcyjności wzajemnych niż amplituda v-tej harmonicznej pochodnej indukcyjności, która w modelu obwodowym będzie wzmocniona rzędem harmonicznej i elektryczną prędkością kątową w.
Literatura
- W. Burlikowski, Comparison of different implementations of reluctance motor simulational model. Proceedings of XLIII International Symposium on Electrical Machines, Poland, Poznań, 2–5 Juny 2007, s. 147–150.
- A. Boboń, S. Paszek, P. Pruski, Wyznaczanie parametrów elektromagnetycznych generatora synchronicznego w środowisku Matlab/Simulink, XV Międzynarodowa Konferencja Naukowa „Aktualne Problemy w Elektroenergetyce”, tom I: Systemy elektroenergetyczne: Stabilność, niezawodność, awarie i restytucje. APE 2011, Gdansk-Jurata, 8–10.06.2011, s. 221–228.
- A. Demenko, L. Nowak, W. Pietrowski, J. Mikołajewicz, Wyznaczanie indukcyjności głównej maszyny indukcyjnej z nasyconym obwodem magnetycznym metodą elementów krawędziowych, „Przegląd Elektrotechniczny” nr 6, 2009, s. 13–16.
- P. Kisielewski, F. L. Antal, Polowo-obwodowy model turbogeneratora. Prace Naukowe Instytutu Maszyn, Napędów i Pomiarów Elektrycznych Politechniki Wrocławskiej, Nr 59 Studia i Materiały Nr 26, 2006.
- K. Ludwinek, J. Staszak, Possibility of graphical environment applications for evaluating of equivalent circuit parameters and time constants, „Przegląd Elektrotechniczny”, 12a. 2011, pp. 195–200.
- K. Ludwinek, Odwzorowanie indukcyjności własnych w modelu obwodowym maszyny synchronicznej jawnobiegunowej, „elektro.info” nr 7–8, 2013, s. 36–41.
- A. Puchała, Dynamika Maszyn i Układów Elektromechanicznych, PWN, Warszawa 1997.
- T. Sobczyk, Metodyczne aspekty modelowania matematycznego maszyn indukcyjnych, Wydawnictwa Naukowo-Techniczne, Warszawa 2004.
- J. Staszak, Kształtowanie charakterystyk elektromechanicznych trójfazowego silnika indukcyjnego klatkowego poprzez dobór uzwojenia stojana oraz układu zasilania. Wydawnictowo Politchniki Świętokrzyskiej, Monografia M31, Kielce 2012.
- S. Wiak, R. Nadolski, K. Ludwinek, J. Staszak, Influence of the Synchronous Cylindrical Machine Damping Cage on Content of Higher Harmonics in Armature Currents During Co-Operation with the Distorted and Asymmetrical Electric Power System, Computer Engineering in Applied Electromagnetism, IOS Press, 2006, pp. 520–527.
- P. Zalas, J. Zawilak, Gentle synchronization of two-speed synchronous motor with asynchronous starting, Electrical Engineering (Berlin). 2012, vol. 94, nr 3, s. 155–163.
- http://www.femm.info/wiki/HomePage